
In the last few days, the community of Information Security experts was shaken by a new attack (dubbed as KRACK) to the WPA2 protocol which is currently protecting the WiFi links for all the devices we love and use in our everyday life such as smartphones, laptops, Smart TVs and so on.
The attack was particularly shocking due to the fact the WPA2 was deemed secure, having resisted through the years to a whole lot of compromise attempts.
But as with any hype, it’s always good to slow down a bit and analyse the actual situation. To do so, we will refer to the original paper.
Whenever a WiFi client (e.g. a smartphone) connects to a WiFi network protected by WPA2 and a pre-shared key (PSK) a handshake protocol takes place in order to establish a common cryptographic key to encrypt the traffic, in order to ensure protection against attacks such as deciphering, packet replay and injection.
This encryption key is called a session key since, after the communication session has been terminated, it’s forgotten and never re-used again (actually, it should be deleted from memory).
The whole handshake protocol happens “in the clear”, i.e. without protection, as the attacker is supposed to be able to observe the data packets that are exchanged between the parties. It may sound scary but that is not a problem at all.
Without giving the details on how to generate such a session key let’s call it temporal key, TK, using WiFi terminology. How is this TK used? There are a number of options, working more or less in the same way. Anyhow, the relevant concept to keep in mind is that the TK should never be used to encrypt the data packet directly as this would expose the traffic to statistical analysis.
I give you an example of this. If we encrypt the traffic by encrypting each bits separately with the TK, the encrypted sequence would look something like:
001011001 → TK(0) TK(0) TK(1) TK(0) TK(1) TK(1) TK(0) TK(0) TK(1)
It’s easy to see that an attacker sniffing such a traffic would be able to guess that the sequence is either 001011001 or 110100110 because the cyphertext would be just a sequence of either the symbol for TK(x) or the one for TK(y), even if she or he wouldn’t be able to tell if x is 0 or 1.
But simply performing some basic statistics (or knowing that at a certain position there is always a pre-defined bit which is 0 or 1) she or he could easily recover the whole sequence, no matter how long the key and how strong the encryption algorithm are.
In order to overcome this difficutly, it’s common to use an encryption key which is specific to every single packet. Hence, we have the following key hierarchy:

From left to right, the lifespan of the encryption key bocomes shorter and shorter. The PSK would be rarely changed (say, once in a month), the TK would be used for the communication session of a single device (for a few hours) while the EK lives only for a packet and then is thrown away (after a few microseconds).
How do we get from the EK to the TK? The key’derivation algorithm is, in fact, pretty simple:
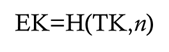
where n is the sequence number of the packet, usually known as the nonce. Let’s keep this term in mind.
H is a one-way hash function and, in this case, we take advantage of the unpredictability of the result: it’s extremely difficult to correlate the input and the output of the function without applying H the input itself. In other words, without knowing the input, the output bits would appear as randomly picked making the sequence of EKs completely uncorrelated (and, in principle, killing any possibility of a statistical attack).
Another way to see this is that if we have input A and B and output C and D corresponding to A and B, we (actually nobody) would not be able to tell whether C = H(A) or C = H(B) without actually applying H.
It should also be noted that while H is unpredictable, it is also totally deterministic: applying H to the same input would
invariably yield the same output.
Racapping, the encryption scheme is the following:

The clearstream will be turned into the cipherstream via a XOR (⊕) operation with the so-called keystream, i.e. the sequence of the EKs.
We can also rewrite the previous scheme using some kind of formal notation:

It’s important to note that in such a scheme it’s of paramount importance to never repeat the same keystream for different sequence of packets. If that is the case, it would be possible to recover a XOR-combination of the clearstreams by leveraging the following properties of the XOR operation:
- Bit 0 is the identity element, i.e. x ⊕ 0 = x.
- Each bit is the inverse of itself, i.e. x ⊕ x = 0.
- XOR is commutative, i.e. x ⊕ y = y ⊕ x, and distributive, i.e. (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z) = x ⊕ y ⊕ z.
In practice, in any formula built out from solely XOR operations, it’s always possible to remove an even number of identical basic operands, whichever the position.
Hence, if two packets are encrypted using the same keystream, an attacker would be able to apply a XOR with the following result:

As already mentioned, the attacker is able to recover a XOR-combination of the two clearstreams which can be further (and more easily) analysed using statstical tools. It should be noted that this specific part of the KRACK attack is not innovative as it was long known.
With this pre-requisite in mind, understanding the inner working of the KRACK attack to WPA2 is relatively simple: in fact, it’s enough to force a WiFi device to re-use the same keystream, applying the trick should above in the final part.
How can this be done?
The KRACK attack shows that it’s possible to manipulate the flow of packets between two devices (namely the Access Point and the client) by mounting a man-in-the-middle attack — and in the article a particularly clever way to do so — to block the packet terminating the handshake so that it never reaches the Access Point.
At that point, the Access Point, according to the WPA2 specification, would resend the last-but-one packet of the handshake which, reaching the client, may force the reset of the nonce which, in turn, would trigger the re-use of the same keystream for the newly generated traffic. I want to underline the term “may” as the behaviour of the WPA2 client upon receiving again the last-but-one packet of the handshake protocol is not specified in the WPA2 itself, leaving this to interpretation. It turns out that most of the implementation of the WPA2 protocols actually resets the nonce.
Now for some considerations:
- The vulnerability can easily be removed by forbidding the clients to reset the nonce — no need to revise the protocol.
- In most of the cases, deciphering the traffic is not immediate as further statistical attacks (which may eventually be unsuccessful) are needed.
- The communications with an HTTPS server (e.g. with your Bank) are protected by an additional layer, i.e. TLS, which is totally independent from WPA2.
What to do, then? Well, first of all, realising that explointing this vulnerability is not as easy as it seems from mainstream news and, under no circumstances, it leads to a compromise of the PSK. In addition, it cannot be mounted from a remote location (i.e. the attacker must be physically present at the location where the attack takes place).
In the second place, patch your devices regularly and you’re pretty most done. And never consider WPA2 a way to protect your traffic from eavesdropper, but only a way to restrict access to the communication channel of your WiFi network. Any sensitive connection should be furtherly protected using additional and much stronger protocols like TLS or SSH.
