
Recently, I got involved in some discussions on the feasibility of a voting scheme which can be untraceable and based on the Blockchain.
The discussions soon polarized between two opposite factions. Nevertheless, in both of them, I noticed a certain lack of knowledge on how Blockchain works and how it could be applied in this specific context. Let’s have a look then.
The discussion stem from a recent referendum in Lombardy in which, for the first time ever in Italy, people were able to express their preference electronically using a tablet inside the voting booth. As one would have expected, this caused a lot of concerns about the reliability of the procedure, invoking scenarios ranging from plot theories to intrusion by Cyber Terrosists… though, the outcome of the vote was overwhelmingly clear to overcome any doubts about these concerns.
Now, the topic of electronic voting is exceptionally complex. Nonetheless we can investigate it for specific aspects without bothering too much about all the details. Namely, the possibility to eliminate a trusted third party to coordinate the operations looks very interesting, as it’s also the rationale behind a lot of plot theories.
If we look at the e-voting problem from the perspective of the Blockchain, there are a lot similarities: the issue of double spending seems to be very close to the one of double voting. Can we exploit the same solutions found to tackle the former to overcome the latter?
At first glance, one could think to re-use the same Blockchain behind the most successful cryptocurrency, Bitcoin. And we could even argue that e-voting is just a smart contract deployed in a suitable environment like Ethereum, the second-largest cryptocurrency.
Compared to these classic cryptocurrencies, there is a difference in the e-voting scenario as both these cryptocurrencies require the full visibility of the transactions by all the parties in order to avoid fraud attempts like double spending.
This specific feature of the classic Blockchains is openly in conflict with the untraceability requirement of anonymous voting.
In other words:
- a party must be authenticated in order to be admitted into the voting cabin.
- an authorized person cannot vote twice (double voting);
- the preference cannot be traced back to the person who casted it.
In Bitcoin and Ethereum it’s of course possible to implement the first two properties only, i.e. you can implement only an open vote where everybody knows the preference casted by anybody else. But we are interested in having the three properties together.
Luckily, there are Blockchains which implement a mechanism similar to cash where money is spent anonymously. Specifically, Monero is one of these (others include ZCash).
There are two substantial differences between Monero and Bitcoin:
- in Bitcoin it’s possible to transfer any amount of money while in the classic version of Monero one can only transfer multiple discrete quantities (tokens), exactly like it happens when you pay in cash; I say “classic Monero” because in the latest versions of its Blockchain there are mechanisms in place that allow to shield the transferred quantity from the eyes of an eavesdropper, enabling the transfer of arbitrary quantitites.
- In Monero, a single transaction is funded from one of multiple wallets but none can tell exactly which one is actually used, implementing an anonymous spending scheme.
How it’s possible to implement the second properties? In practical terms, Monero Blockchain implements a mixing scheme in which identical transactions from different wallets are mixed together so one cannot trace back to a specific wallet.
In the following figure we can see a classic mixing scheme, as the one implemented in many Bitcoin coin tumblers:

On the left we see three different transactions. These transactions are then handed to a “mixer” (the blue square) which merges the three of them to create a single transaction with multiple inputs and multiple outputs. In this mxing scheme is of paramount importance that the transferred quantities are the same across all the transactions, otherwise one would be able to tell which sender’s wallet is sending money to which recipient’s wallet.
Coin tumblers mixing Bitcoin transactions are not new and were actually pretty common. On the Darknet (i.e. TOR Hidden Services) one could buy illegal substances from drug dealers paying in bitcoins which were previously “cleaned” by one or multiple mixer services. It’s needless to say that such mixers were a single-point-of-failure as they could disappear stealing the money in the transactions as well as be seized by the authorities and forced to reveal the actual underlying transactions.
In Monero this relevant issue is overcome by forcing the sender to mix other similar unspent transactions with his own in order to make it untraceable. The mixed transactions are not actually spent like in a classical tumbler, they are only used to hide the actual transaction. This way of working is also known as spontaneous mixing.
Hence, in order to transfer x tokens in Monero we follow this simple procedure:
- we choose randomly N>1 wallets which contains exactly x tokens;
- we create a transactions which is sourced from these N wallets: only one of these wallets is actually used and, thus, only x tokens are transferred (instead of N·x like in a classical tumbler).
The spending scheme is shown in the following picture:
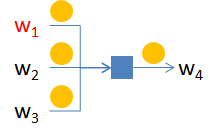
Wallet w1, marked in red, is the one owned by the sender but to an external observer this cannot be pinpointed since any of the wallets could be the one involved in the spending transaction.
At this point, one last element is needed for the e-voting scheme to work: how do we authenticate the transaction in order to check that it’s legitimate? We cannot use a classic signing scheme as this would allow the external observer to identify the sender’s wallet immediately.
This problem is solved using a different signing scheme called ring signatures.
In a classic signing scheme, the verifier V is able to validate the signature by checking that the signature S is consistent with the public key P:
Using a ring signatures this relation is turned into the following:
In this case, the verifier V knows that S in consistent with the set of public keys on the right-hand side but will not know to which of these it belongs to.
In Monero, each transaction is signed with a ring signature and the miner will be able to check that, in fact, one of the owners of the wallets signed the transaction without being able to tell which one specifically.
This is not enough, yet. It’s still possible to perform a double spending as a previous spender could replicate N times the same transaction and, each time, this validates until all the tokens in all the wallets are spent.
This difficulty is overcome introducing a slightly modified version of the ring signatures adding the property that any signer using the same private key twice would be uniquely identified.
At this point, implementing an untraceable voting scheme is almost trivial.
To make things simple, let’s assume that the voter can cast one out of two possible preferences, either “A” or “B” (this is the case of a referendum where one votes for or against a proposal). The scheme works in this way:
- the voter creates two tokens in its wallet, one for A and the other for B. Any single voter would be allowed to do so only once;
- the voter creates a third token, Δ;
- in order to cast its preference, the voter creates a transaction which is spontaneously mixed with a number of other transactions casting the same vote of the form
where
is either A or B. Spending Δ along with one of the preference avoids that the voter can cast another vote with the other preference.
- Once the referendum terminates, each voter can count autonomously how many As or Bs were casted and know the outcome of the poll.
As said before, in order for this scheme to work, each voters will have to create identical tokens A, B and Δ.
As described, the scheme shows the following properties:
- the vote cannot be traced back to the actual caster because of the spontaneous mixing;
- the voter (identified by her/his public key) can vote only once because the tokens A, B and Δ can be created only once and this rule will be enforced by the miners validating the transactions;
- voters cannot cast both votes because only one Δ token is available.
Lastly, if we are using a non-permissioned blockchain, the list of the admitted voters must be publicly available.
In conclusion, this small article is showing how the Blockchain could be applied to very diverse problems, not being limited to cryptocurrencies.
In the specific case of e-voting scenarios, it’s also pretty clear that it’s not enough. Even if the Blockchain eliminates the need to trust a central third party to coordinate and declare the final outcome, it’s also true that parties will have to trust the writer of the voting software, who would be able to inject backdoors in order to compromise the confidentiality and the integrity of the elections.
