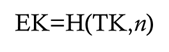My recent articles – XOR ⊕ GURU

March 18, 2019March 18, 2019

Cryptographic “Heads and Tails” and privacy-preserving blockchains

Sometime, the technology behind the Blockchain appears to be out of reach for the common man. Yet, I have a passion in trying to explain the “hard concepts” in simple terms and in this one I will touch upon the idea behind privacy-preserving blockchains like ZCash or Monero.

To do that, we will talk about Heads and Tails.

Heads and Tails over the phone

Suppose you want to play “Heads and Tails” with one of friends that’s living oversea. Also, let’s say that you live in the 80s with no possibilities to have a video conference with your friends whatsoever.

You then arrange to play over the phone: your friends will toss the coin and you’ll do the bet. So, things go like this:

You tell your friend your bet.
Your friend toss the coin and tells you the outcome.

Of course, this very simple protocol is subject to be abused, namely by your friend, since he will have the chance to tell you whichever outcome is beneficial for him, i.e. the opposite of your bet.

The only way it can work is that you trust your friend. Still, you have no concrete ways to conclude that he’s actually cheating or not.

Adding some crypto

In a way, cryptography is all about minimizing (or possibly eliminating) trust from a certain “mechanism”, it being the transmission of a message, a protocol etc.

In this specific case, we want to minimize the need to trust our friend. So we need to find way to forbid him to cheat or, at least, to detect when he does it, at least with a certain probability.

In order to do this, we will make use of a commitment scheme. In simple terms, a commitment scheme is a way for a party to hide a message from the sight of the other parties with no possibility for him to change it later on. It’s pretty much like putting the message in a sealed envelope and giving the envelope to the other party.

A commitment scheme is made up of two parts:

Hiding. The message is hidden using a function f. The easiest function is a one-way hash function. So, the commitment c becomes H(m). c is then sent by the committer to the other party, called the verifier.
Opening or Revealing. The committer sends the message m to the verifier, possibly along with some other information I, to convince him that the message m was indeed the one hidden in c. In the case of a one-way hash function I is simply empty and the verifier just recalculate c = H(m).

With this in mind, let’s see the revised protocol:

Your friend picks a random number n (a nonce).
Your friend then tosses the coin with outcome r.
Your friend hashes n and r together, forming a commitment c = H(n | r) which is sent to you.
Now you make the bet and tell your friend about it.
Your friend sends n and r to you to convince that c = H(n | r).

In this scheme, none of the two parties can cheat: Your friend cannot change the commit after it was sent to you and you don’t learn anything about the outcome r from the commitment c.

Since this scheme cannot be cheated, we actually removed any need of trust between the two parties. It’s important to note that the nonce n is needed for this to work otherwise you just try to hash the two possible outcomes, H(head) and H(tail), and then it would be straightforward for you to learn which of the two outcomes is hidden in c.

Notice that the scheme can also be played as follows:

You pick a nonce n and make a bet b, hashing the two together as c = H(n | b) and then sending it to your friend.
Your friend then tosses the coin with outcome r, which is communicated to you.
You send your friend n and b to convince that c = H(n | b).

This works as well but this time you would be the committer.

“Heads and Tails”: solo version

Let’s say now that you and your friend decide to play N times the game of Heads and Tails. Using the above protocol, there would be a need to perform 3N communications between you and your friend, which is not ideal.

On top of that, now suppose that there is a third party, the payer. Basically, after the game is run N times, you go to the payer in order to get the reward which would of course depend on how many rounds you won.

But, then, there is a problem. How can the payer be sure that you didn’t collude with your friend to split the reward? You cannot just present it the script of the above protocol to the payer.

In general, this means that the protocol above cannot be publicly verified.

In order to make the protocol work under these settings, we need to change it a bit. Basically we would play a solo version of the protocol where you toss the coin by yourself and present the results to anyone interested in seeing it (e.g. your friend and the payer).

But how can one be sure that you played honestly when you are, at the same time, the one who’s betting and the one who’s tossing the coin?

It turns out that this is indeed possible, exploiting the fact that a one-way hash function is kind of splitting a sequence of the events in a “before” and an “after”: If d = H(m) then m must have been chosen before we knew d since H() is one-way and you cannot reverse it (i.e. you cannot reverse time).

Fiat and Shamir showed that this property can fruitfully be used to turn interactive protocols into non-interactive publicly verifiable protocols.

Here’s how it works:

Everybody agrees on a random value x which is called a public coin. This step is really important otherwise you could use a previous sequence of bets that you know are favorable for you.
You now choose N bets, one for each round. Let’s represent these bets as a sequence b of N bits, where a 0 in the k-th position means that your bet is a head for the k-th round (and 1 for the tail, of course).
Now you calculate r = H(x | b). These represent the results at each round: If the k-th bit of r is 0, it means that the outcome for the k-th round would be a head (and 1 for tail, like before).

Now you go to the verifier and the payer and present them b and r. They would simply recalculate r = H(x | b) and, in case it matches, it means that you played honestly and can get your reward.

Why this protocol works?

Since H() is one-way, you cannot “predict” r before “tossing” the hash from b.

Technically speaking, a hash function is approximating a random oracle. In simple terms, a random oracle is a function which is always returning the same output given the same input. But the oracle will pick the output randomly the first time it sees it, giving the same result from that moment on. So, again, you cannot know the randomly picked number before asking the random oracle.

In other terms, finding the b which is giving a pre-defined r would be as hard as inverting the hash function. Put it in another way, this would be equal to solving this equation:

$H(b) \oplus{} b = 0$

which requires to invert H to be solved for b.

But there is a caveat to this.

The verifier and the payer can only be sure that you played honestly with a certain probability. It means that there is still a chance for you to cheat the protocol. But this chance can be made negligible if N is sufficiently large.

For the specific case of Heads and Tails, this caveat works as follows.

Since H() is much like a uniformly distributed random variable, on average, you would win 50% of the rounds, sometime more, sometime less. Can you increase this probability?

Let’s suppose that the sequence of bets is b = b0 | b’, i.e. we are specifically looking at the first bet. We can then calculate r = r0 | r’ = H(x | b0 | b’), looking specifically at the first result r0. Regardless of the b0 and r0, since H() is uniformly distributed, on average, the outcomes for b’ would be still 50% favorable to us.

For the first bet b0 the following may happen:

For any b0, we always lose if r0 ≠ b0.
For any b0, we always win if r0 = b0.
b0 = r0 (we win) if either b0 = 0 and r0 = 0 or b0 = 1 and r0 = 1

In case of 2, we just pick head or tail and we are sure to win. In case of 3, we pick the bet where we win. For 1, well, we try to flip another bet :-).

It turns out that we have increased the chance to win the first bet from 50% to 75% and, on average, the winning rounds above 50%. How much? Well, it depends on how large is N.

We can also extend this strategy to other bets but then we must check 2^n hashes and, with n sufficiently large, this would quickly become as impractical as reversing H(). In order to stay on the safe side N should be twice the length of the digests.

Bottom line: we can work out a version of the protocol that’s publicly verifiable and it’s not interactive, but it comes at a cost of requiring that N must be very large.

Enter the Blockchain

What this solo “Heads and Tails” has to do with blockchains?

In privacy-preserving blockchains, i.e. those where transaction content is kept confidential, one must prove to the miners that a transaction is not violating the rules set out for the blockchain, i.e. basically not spending more money than those found in the wallet, without revealing anything of the underlying content of the transaction.

In order to do this, a protocol very similar to the one described above for Heads and Tails is applied. Specifically, we will refer to the second version of the commitment-based interactive protocol.

So, first of all, there will be the creator of a transaction T which will be “encrypted” so nobody can look into it. This is similar to picking head or tail and committing to it via hashing in our “Heads and Tails” interactive protocol.

Let’s now imagine that we have a miner who needs to validate the transaction T. Since it’s encrypted, he cannot check that it’s correct directly. So, the creator of the transaction engages a dialogue with the miner in order to convince him that T is, indeed, valid. Hence, the miner starts a series of questions to which the creator replies.

The most basic question that the miner could ask is “can you show me the content of the transaction?”, which is similar to having the better sending the bet to the verifier in the interactive Heads and Tails protocol.

Of course, the creator of T will never answer such a question since he doesn’t want to reveal the content of the transaction. This represents an important difference compared to the simple Heads and Tails protocol since the miner must not learn anything about the content of the transaction. It’s said that the dialogue is run in zero-knowledge.

So, the miner asks a different kind of questions which are able to signal to him whether the creator knows T and that T is correct, up to a certain probability, let’s say 50%.

But the miner wants to be very sure that creator of T was not just lucky in answering correctly to the question asked. So he asks another question. The probability of correctly answering both questions without knowing the content of T and convincing that T is correct drops now to 25%.

Hence, the miner will go on with asking questions until this percentage drops to an acceptable amount. In practice, the miner randomly generates a number that is used to build the next question. In the end, the miner will ask Nquestions after which he’s convinced that the creator knows the content of Tand that T is correct, exactly like tossing the coin N times in the non-interactive version of Heads and Tails convinces the verifier that the better didn’t cheat.

The script of this dialogue between the miner and the creator of the transaction is then a sort of “proof” that T is correct, but this proof only works for that specific miner.

Therefore, such an interactive protocol is not suitable in a blockchain context where transactions need to be proved correctly to all the miners: If we had to do it really interactively, the creator would have to talk to each miner separately, with a unique dialogue, to convince each of them that the transaction is correct. This is, of course, impossible to do, considering also the asynchronous context of a blockchain.

So, Fiat-Shamir heuristic can be used to turn the dialogue between the miner and the creator of T to a non-interactive publicly-verifiable proof that the transaction is correct, “simply” by replacing the random number generator used to build the questions asked by the miner with a one-way hash function.

As we saw, this trick works but it turns out to be heavier than in traditional blockchains since proofs of correctness are, in fact, much longer.

Therefore, much of the research in this field is devoted to producing proofs that are as short as possible and to making the validation algorithm of such proofs as quick as possible.

March 9, 2019March 11, 2019

Practical auditable elections with deferred parallel consensus

Recently, a few friends of mine have come back to me after reading my previous articles about elections on the Blockchain (part 1 and part 2 ). They were wondering how feasible it would be to implement a voting scheme that works in the real world.

Some of the requirements I got from them are the following:

The voting platform must scale on the number of voters.
The whole voting process must support short-lived elections, i.e. a few hours or, in some extreme cases, even minutes (think of a poll in a TV show).
Minimal to no trust should be put in any of the party involved in the voting process.
It must not be possible to trace the ballots back to the actual individual voters.
Honest voters must be ensured that their vote will be taken into account during the final tallying.

As you can see, these requirements are pretty challenging: while the “no trust” requirement would make us lean towards a Blockchain-based solution, the possibility to scale to thousands of transactions per seconds seems to rule it out.

As a first attempt, we will go then for a hybrid solution based, both on a centralized setup (for scalability) and a public Blockchain (to keep integrity and auditability) as well as on a private Blockchain to reach consensus on the final results. To design the solution, I took inspiration from the Google’s Certification Transparency Initiative and this paper by Liu et al which introduced the concept of Linkable Spontaneous Anonymous Group (LSAG) signatures.

For the time being, we won’t take into account the problem of vote-selling or vote-coercion.

Electronic voting: still a Chimera

A huge caveat to this article. Full electronic voting has still a lot of road to do. Many problems found a solutions but issues are still standing out there.

One of the trickiest is software integrity: How do we ensure that the software you are using for voting (e.g. an app on a smartphones or a tablet in the polling station) has not been tampered with by an attacker? Marking a ballot with an “X” is a lot easier to verify than checking that an encrypted vote is actually the one you intended to cast. On this topic, I would suggest reading a nice essay by Ronald L. Rivest.

Linkable Spontaneous Anonymous Group (LSAG) signatures

A cornerstone of the solution described in this article are LSAG signatures. In practical terms, a LSAG signature allows to hide the signer’s identity among a group of other identities. A verifier will not be able to identify the actual signer but be sure that the signature has been performed by one of the group members. In addition, an LSAG signature scheme allows a verifier to “link” signatures that have been generated by the same identity which, nevertheless, remains anonymous (or pseudonymous). A LSAG signature has this form:

where s is the signature of message m, G is the group of identities among which the actual signer is concealed, L is the “signer’s link” which is uniquely bound to the signer without revealing her/his real identity, i.e. it cannot be changed by the signer but the signer’s identity cannot be (computationally) derived from L. In this article we will refer to the LSAG as described in Monero’s Confidential Transactions paper by Noether. Specifically, L will not depend on G.

Crypto-currencies and e-voting: a difference in scope

Double spending and double voting seem to be pretty much the same problem: you don’t want a party to spend the same coin twice, the same way you don’t want a voter to cast two or more (possibly contradictory) ballots.

Nevertheless, there are two important differences:

Commutativity. There are no specific ordering requirements for the votes expressed during an elections. In the end, the final result doesn’t depend on whether vote A arrived before vote B (or viceversa).
Independence. Casting a ballot by a voter is done in isolation: the ballot cast by a voter is not influenced by the ballots previously sent by any other voter. On the other way around, in the context of payments, a coin can be spent only if previously received by another party (or mined).

Somewhat, between payments and voting, there is a difference in scope. Spending is a global-scope activity: everybody must be informed of a party spending a coin to avoid double spending. This holds true also in non blockchain-based financial systems: the global scope is usually maintained in a few core systems, like TARGET2 in the Euro area.

Conversely, voting is basically local-scope: casting a vote doesn’t have any dependency on the other castings performed by the community, the only requirement being that the tallying authority must be able to rule out double votes, either by prevention or by detection.

This difference in scope allows an election to be split into independent sub-elections. By the way, this is not different from what’s happening in the real world where voters express their ballot into different and independent polling stations. Also, the final aggregation does not depend on the order in which votes are received: they are thrown into a voting box where order is not preserved.

On top of that, we will see that the local-scope of voting scheme allows to defer the consensus phase at a later stage, just before the tallying.

A practical scheme

Environment

In the environment where the elections take place the following components are available:

The Authoritative Node. This is a server that is publicly accessible and is designated in this role by the party that is starting the election, the Polling Authority.
Witness Nodes. These are a number of servers that are publicly accessible. The Witness Nodes is an open set and any party is invited to join.
A public Blockchain. All the parties have complete and unrestricted access to a public, non-permissioned Blockchain (e.g. Ethereum). The messages sent to the Blockchain cannot be tampered with by any of the parties involved in the election process. Also, the Blockchain is acting like a provable public clock with time provided in the form of the block number and proof as the block digests.
The Polling Authority. This party designates the Authoritative Node and ensures the registration of Voters and the Witness Nodes. Also, the Polling Authority transitions the election process into the different phases and, finally, declares the outcome of the election. The public key of the Polling Authority is known to all the parties.

We also assume that all communications between the parties happens in an anonymous fashion, e.g. using the Tor mixing network.

Registration phase

First of all, the Polling Authority publishes in the Authoritative Node a random number, the PollID, that uniquely identifies the current election, along with a public key, the Poll Public Key . Also, the Polling Authority publishes the list of the possible votes that can be selected by the voters for the current election. For this article we will assume a referendum-like election, i.e. the voter can choose only between two mutually-exclusive votes, indicated as 0 and 1. The PollID, the Poll Public Key and the choices are signed by the Polling Authority.

In this phase, Voters go to the Polling Authority and present their identity along with a public key in order to be registered as voters. The Polling Authority has the right to reject a Voter if she/he is not eligible to vote in the current election. Upon successful registration, the Polling Authority releases a signed Registration Receipt to the Voter containing:

The Voter’s identity.
The Voter’s public key.
The PollID.
The current time from the public Blockchain.

Also, in this phase, the Witness Nodes are registered with the same mechanism: an identity and a public key is provided by the party managing the Witness Node and a signed Registration Receipt is released with the same elements as above. For the Witness Nodes, a publicly accessible URI is provided which will be later used during the voting phase by the Voters.

After the registration phase ends, the Polling Authority publishes the list of Voters and the list of Witness Nodes in the Authoritative Node, both in terms of identity and public key. For the Witness Node, the voting URI is also published.

Merkle Tree Hashes of the list of Voters and the Witness Nodes are published to the Blockchain, along with the PollID and the possible votes. These digests are signed by the Polling Authority. For now on, Merkle Trees contain leaves represented by the pair (n,L) where n is the position of the node L in the list.

In case a Voter or a Witness Node is not appearing in the published lists, she/he can use the Registration Receipt to object. Also, the honest Polling Authority can always provide a membership proof for a Voter or Witness Node that can be publicly verified in order to counteract false claims of registration rejections.

After this phase and at a convenient time, the Polling Authority declares the opening of the election. This transition is signaled to the public Blockchain.

Voting phase

A Voter encodes a message containing his voting preference following these steps:

The Voter accesses the Authoritative Node to pick randomly N identities from the public list of Voters. For each identity, the information received from the Authoritative Node is the public key and a membership proof based on the Merkle Tree Hash published in the public Blockchain by the Polling Authority that the identities are actually in the list of Voters. We call this set the Signature Group. Notice that, by using membership proofs, the voter avoids downloading the whole list of voters just to pick some identities randomly. In fact, the voter inquiries the Authoritative Node (via a proper API) and can be ensured that the identities retrieved are part of the list of Voters. In addition, this information must be publicly available, i.e. there must be no need to provide an authenticated identity to perform queries to the Authoritative Node. In this way, we avoid identity fingerprinting by the composition of the group G in the LSAG. Finally, the Authoritative Node must return exactly those identity requested by the voter: recall that the leaves of the corresponding Merkle Tree contains, indeed, the position of the leaf in the tree.
The Voter selects a number of Witness Nodes from the list published in the Authoritative Node. Like in the previous step, the Voter receives the public keys and the membership proof that the selected Witness Nodes are registered as such in the Authoritative Node, consistently with the Merkle Tree Hashes published in the Blockchain.
The Voter gathers the possible votes that are available for this election from the Authoritative Node along with the Poll Public Key.
The information gathered in 1, 2 and 3 are checked for authenticity against the Polling Authority’s public key. Information gathered in 1 and 2 are also verified for integrity using the Merkle Tree Hashes published in the public Blockchain.
The Voter pick one of the votes, encrypts it with the Poll Public Key along with a random nonce (to ensure uniqueness of the encrypted vote) and prepares an LSAG signature using the Signature Group as defined in 1. These information, together, form the ballot.
The Voter sends her/his ballot to the Authoritative Node and to all the Witness Nodes selected in 2.
The Voter receives back a signed Ballot Receipt which acknowledges that the ballot was received by the Authoritative/Witness Node. Among the other information in the receipt, the Voter receives the ID of the block in which his ballot was inserted and the position k in the sequence of ballot in the block (see later).

When the Authoritative/Witness Node receives the ballot from the Voter:

It checks the eligibility of the identities in the Signature Group by looking up the list of voters. Alternatively, the voter can provide the membership proofs received previously by the Authoritative Node.
It checks the validity of the LSAG signature.
It checks that no previous ballot was received from the same voter by looking up the signer’s link in the LSAG signature in the cast ballots. Notice that the anonymity of the voter is still preserved even if two such ballots are found.
It inserts the ballot in the current partial block of ballots.
Prepares and signs a Ballot Receipt with the following information:
- the current time (taken from the public Blockchain) when the vote was received by the Authoritative/Witness Node,
- the unique ID of the current partial block,
- the position k in the block in which the ballot is inserted,
- a signed digest obtained by hashing these information along with the ballot and the LSAG signature.
Upon receiving the Ballot Receipt, the Voter checks the authenticity, the integrity and the freshness of the receipt.
The Authoritative/Witness Node finalizes the current partial block of ballots by sending the Merkle Tree Hash to the Blockchain, along with the block ID and the identity of the Authoritative/Witness Node. The Voter can request a membership proof of her/his vote from the Authoritative Node and the Witness Nodes. This request is performed by specifying the index k provided in step 5. The anonymity of the Voter is preserved since this information can be publicly inquired.

After a certain amount of time the Election Authority declares that the election is over by signaling this in the Blockchain.

Consensus phase

In this phase, the Authoritative Node and the Witness Nodes cooperates to reach consensus on the complete list of the ballots received for the election. In principle, the Authoritative Node should already have all the ballots expressed by the voters Nevertheless, we cannot exclude a malicious behavior of the Authoritative Node, considering that the Polling Authority knows the votes contained in the ballots received. The Authoritative Node cannot, of course, forge the ballots nor change their content but it may still be able to omit a ballot.

Let’s then suppose that a Voter sends her/his ballot to the Authoritative Node. The Voter receives back the Ballot Receipt and, once the Merkle Tree Hash of the block containing the node has been published to the public Blockchain, the Voter inquiry the Authoritative Node to check that in position k of block N her/his vote has been actually included.

What happens if the Authoritative Node returns a membership proof that doesn’t match the Ballot Receipt? The Voter may be willing to raise an objection, maybe going to higher level authorities. But, doing so, the Voter must be obliged to disclose her/his identity in reference to that particular ballot, something that the Voter is unwilling to do. The Authoritative Node may then play with this fact to actually try and omit that ballot.

To avoid this situation, the Witness Nodes come to play. If a ballot is received by multiple Witness Nodes, we hope that at least one of them notices that the vote has been omitted, trying and reinserting it in the final set of tallied ballots: this way, the Voter doesn’t need to disclose her/his identity. Notice that a Witness Node doesn’t know the Poll Private Key and cannot decrypt the votes. In addition, we assume that the Witness Nodes have different and conflicting interests. For example, the Witness Nodes can be run by the different parties running in an election and by the press that is following the event.

One may also argue that receiving the Ballot Receipt and the subsequent membership proof is pointless with this scheme. In a sense, this is true but they can be used by the Voter to sequentially select the Witness Nodes until one of those confirms that the ballot has been received. Basically, the Voter retrieves the first Witness Node and sends the ballot to it. After the Witness Node publishes the hash of the corresponding block to the public Blockchain, the Voter check that her/his ballot has actually been inserted in the block. If it is, the Voter stops. If not, the Voter select another Witness Node and tries again.

Let’s see how the consensus is reached on the list of ballots. The consensus algorithm works as follows:

Each ballots is assigned to a group. The group the ballot is assigned to is determined by taking the n least significant bits of the digest produced from the ballot using a cryptographic one-way hashing function H, i.e. LSBn(H(ballot)).
For each group of ballots, a private/permissioned proof-of-authority Blockchain is setup among the Authoritative Nodes and the Witness Nodes. The blocks are built as follows:
- The genesis blockchain block is proposed by the Authoritative Node. The genesis block contains all the ballots in the group along with: 1) the ballot hash H, 2) the block ID N of the block published to the public Blockchain by the Authoritative Node that contains the ballot, 3) the position k of the ballot in block N.
- The subsequent blocks are appended by the Witness Nodes and contain the ballots that are missing from the previous blocks (if any) and belongs to the current group, along with the H, N and k for the Witness Node. These latter information is also provided for all the ballots in the previous blocks.
- As soon as all the Witness Nodes appended a block or when a certain point in time has been reached, the Authoritative Node append a closing block to the Blockchain. The content of the closing block is just the current block digest in the public Blockchain.

Practically, there would be a number of private/permissioned blockchains running in parallel. Once consensus has been reached in all blockchains, the ballots received are then used by the Authoritative/Witness Nodes to calculate the Merkle Tree Hashes for each block generated by the Authoritative Node and the Witness Nodes and comparing the hashes with the ones published in the public Blockchain.

Tallying phase

The Authoritative Node activates the tallying by publishing the Poll Private Key in the public Blockchain. At this point, the Witness Nodes and the Authoritative Node decrypt the votes in the ballots and start the tallying. At the end, the Authoritative Node declares the final winner. If this declaration is in contrast with the set of ballots agreed upon by the Authoritative Nodes and the Witness Nodes during the consensus phase, any Witness Node can always publicly object.

That’s it!

Next steps

This scheme will be analyzed in terms of attack scenarios in a later article. In addition, variations of the scheme will be presented.

October 25, 2017September 19, 2018

Blockchain and electronic voting

Recently, I got involved in some discussions on the feasibility of a voting scheme which can be untraceable and based on the Blockchain.

The discussions soon polarized between two opposite factions. Nevertheless, in both of them, I noticed a certain lack of knowledge on how Blockchain works and how it could be applied in this specific context. Let’s have a look then.

The discussion stem from a recent referendum in Lombardy in which, for the first time ever in Italy, people were able to express their preference electronically using a tablet inside the voting booth. As one would have expected, this caused a lot of concerns about the reliability of the procedure, invoking scenarios ranging from plot theories to intrusion by Cyber Terrosists… though, the outcome of the vote was overwhelmingly clear to overcome any doubts about these concerns.

Now, the topic of electronic voting is exceptionally complex. Nonetheless we can investigate it for specific aspects without bothering too much about all the details. Namely, the possibility to eliminate a trusted third party to coordinate the operations looks very interesting, as it’s also the rationale behind a lot of plot theories.

If we look at the e-voting problem from the perspective of the Blockchain, there are a lot similarities: the issue of double spending seems to be very close to the one of double voting. Can we exploit the same solutions found to tackle the former to overcome the latter?

At first glance, one could think to re-use the same Blockchain behind the most successful cryptocurrency, Bitcoin. And we could even argue that e-voting is just a smart contract deployed in a suitable environment like Ethereum, the second-largest cryptocurrency.

Compared to these classic cryptocurrencies, there is a difference in the e-voting scenario as both these cryptocurrencies require the full visibility of the transactions by all the parties in order to avoid fraud attempts like double spending.

This specific feature of the classic Blockchains is openly in conflict with the untraceability requirement of anonymous voting.

In other words:

a party must be authenticated in order to be admitted into the voting cabin.
an authorized person cannot vote twice (double voting);
the preference cannot be traced back to the person who casted it.

In Bitcoin and Ethereum it’s of course possible to implement the first two properties only, i.e. you can implement only an open vote where everybody knows the preference casted by anybody else. But we are interested in having the three properties together.

Luckily, there are Blockchains which implement a mechanism similar to cash where money is spent anonymously. Specifically, Monero is one of these (others include ZCash).

There are two substantial differences between Monero and Bitcoin:

in Bitcoin it’s possible to transfer any amount of money while in the classic version of Monero one can only transfer multiple discrete quantities (tokens), exactly like it happens when you pay in cash; I say “classic Monero” because in the latest versions of its Blockchain there are mechanisms in place that allow to shield the transferred quantity from the eyes of an eavesdropper, enabling the transfer of arbitrary quantitites.
In Monero, a single transaction is funded from one of multiple wallets but none can tell exactly which one is actually used, implementing an anonymous spending scheme.

How it’s possible to implement the second properties? In practical terms, Monero Blockchain implements a mixing scheme in which identical transactions from different wallets are mixed together so one cannot trace back to a specific wallet.

In the following figure we can see a classic mixing scheme, as the one implemented in many Bitcoin coin tumblers:

On the left we see three different transactions. These transactions are then handed to a “mixer” (the blue square) which merges the three of them to create a single transaction with multiple inputs and multiple outputs. In this mxing scheme is of paramount importance that the transferred quantities are the same across all the transactions, otherwise one would be able to tell which sender’s wallet is sending money to which recipient’s wallet.

Coin tumblers mixing Bitcoin transactions are not new and were actually pretty common. On the Darknet (i.e. TOR Hidden Services) one could buy illegal substances from drug dealers paying in bitcoins which were previously “cleaned” by one or multiple mixer services. It’s needless to say that such mixers were a single-point-of-failure as they could disappear stealing the money in the transactions as well as be seized by the authorities and forced to reveal the actual underlying transactions.

In Monero this relevant issue is overcome by forcing the sender to mix other similar unspent transactions with his own in order to make it untraceable. The mixed transactions are not actually spent like in a classical tumbler, they are only used to hide the actual transaction. This way of working is also known as spontaneous mixing.

Hence, in order to transfer x tokens in Monero we follow this simple procedure:

we choose randomly N>1 wallets which contains exactly x tokens;
we create a transactions which is sourced from these N wallets: only one of these wallets is actually used and, thus, only x tokens are transferred (instead of N·x like in a classical tumbler).

The spending scheme is shown in the following picture:

The mixing scheme of Monero: whom the transferred token belongs to?

Wallet w1, marked in red, is the one owned by the sender but to an external observer this cannot be pinpointed since any of the wallets could be the one involved in the spending transaction.

At this point, one last element is needed for the e-voting scheme to work: how do we authenticate the transaction in order to check that it’s legitimate? We cannot use a classic signing scheme as this would allow the external observer to identify the sender’s wallet immediately.

This problem is solved using a different signing scheme called ring signatures.

In a classic signing scheme, the verifier V is able to validate the signature by checking that the signature S is consistent with the public key P:

$\textrm{V}(S)=\textrm{P}$

Using a ring signatures this relation is turned into the following:

$\textrm{V}(S)=\{ \textrm{P}_1, \textrm{P}_2, \cdots , \textrm{P}_n \}$

In this case, the verifier V knows that S in consistent with the set of public keys on the right-hand side but will not know to which of these it belongs to.

In Monero, each transaction is signed with a ring signature and the miner will be able to check that, in fact, one of the owners of the wallets signed the transaction without being able to tell which one specifically.

This is not enough, yet. It’s still possible to perform a double spending as a previous spender could replicate N times the same transaction and, each time, this validates until all the tokens in all the wallets are spent.

This difficulty is overcome introducing a slightly modified version of the ring signatures adding the property that any signer using the same private key twice would be uniquely identified.

At this point, implementing an untraceable voting scheme is almost trivial.

To make things simple, let’s assume that the voter can cast one out of two possible preferences, either “A” or “B” (this is the case of a referendum where one votes for or against a proposal). The scheme works in this way:

the voter creates two tokens in its wallet, one for A and the other for B. Any single voter would be allowed to do so only once;
the voter creates a third token, Δ;
in order to cast its preference, the voter creates a transaction which is spontaneously mixed with a number of other transactions casting the same vote of the form $\left( \textrm{X}, \Delta \right)$ where $\textrm{X}$ is either A or B. Spending Δ along with one of the preference avoids that the voter can cast another vote with the other preference.
Once the referendum terminates, each voter can count autonomously how many As or Bs were casted and know the outcome of the poll.

As said before, in order for this scheme to work, each voters will have to create identical tokens A, B and Δ.

As described, the scheme shows the following properties:

the vote cannot be traced back to the actual caster because of the spontaneous mixing;
the voter (identified by her/his public key) can vote only once because the tokens A, B and Δ can be created only once and this rule will be enforced by the miners validating the transactions;
voters cannot cast both votes because only one Δ token is available.

Lastly, if we are using a non-permissioned blockchain, the list of the admitted voters must be publicly available.

In conclusion, this small article is showing how the Blockchain could be applied to very diverse problems, not being limited to cryptocurrencies.

In the specific case of e-voting scenarios, it’s also pretty clear that it’s not enough. Even if the Blockchain eliminates the need to trust a central third party to coordinate and declare the final outcome, it’s also true that parties will have to trust the writer of the voting software, who would be able to inject backdoors in order to compromise the confidentiality and the integrity of the elections.

October 19, 2017September 18, 2018

Considerations on WiFi and WPA2 – The KRACK attack

In the last few days, the community of Information Security experts was shaken by a new attack (dubbed as KRACK) to the WPA2 protocol which is currently protecting the WiFi links for all the devices we love and use in our everyday life such as smartphones, laptops, Smart TVs and so on.

The attack was particularly shocking due to the fact the WPA2 was deemed secure, having resisted through the years to a whole lot of compromise attempts.

But as with any hype, it’s always good to slow down a bit and analyse the actual situation. To do so, we will refer to the original paper.

Whenever a WiFi client (e.g. a smartphone) connects to a WiFi network protected by WPA2 and a pre-shared key (PSK) a handshake protocol takes place in order to establish a common cryptographic key to encrypt the traffic, in order to ensure protection against attacks such as deciphering, packet replay and injection.

This encryption key is called a session key since, after the communication session has been terminated, it’s forgotten and never re-used again (actually, it should be deleted from memory).

The whole handshake protocol happens “in the clear”, i.e. without protection, as the attacker is supposed to be able to observe the data packets that are exchanged between the parties. It may sound scary but that is not a problem at all.

Without giving the details on how to generate such a session key let’s call it temporal key, TK, using WiFi terminology. How is this TK used? There are a number of options, working more or less in the same way. Anyhow, the relevant concept to keep in mind is that the TK should never be used to encrypt the data packet directly as this would expose the traffic to statistical analysis.

I give you an example of this. If we encrypt the traffic by encrypting each bits separately with the TK, the encrypted sequence would look something like:

001011001 → TK(0) TK(0) TK(1) TK(0) TK(1) TK(1) TK(0) TK(0) TK(1)

It’s easy to see that an attacker sniffing such a traffic would be able to guess that the sequence is either 001011001 or 110100110 because the cyphertext would be just a sequence of either the symbol for TK(x) or the one for TK(y), even if she or he wouldn’t be able to tell if x is 0 or 1.

But simply performing some basic statistics (or knowing that at a certain position there is always a pre-defined bit which is 0 or 1) she or he could easily recover the whole sequence, no matter how long the key and how strong the encryption algorithm are.

In order to overcome this difficutly, it’s common to use an encryption key which is specific to every single packet. Hence, we have the following key hierarchy:

From left to right, the lifespan of the encryption key bocomes shorter and shorter. The PSK would be rarely changed (say, once in a month), the TK would be used for the communication session of a single device (for a few hours) while the EK lives only for a packet and then is thrown away (after a few microseconds).

How do we get from the EK to the TK? The key’derivation algorithm is, in fact, pretty simple:

where n is the sequence number of the packet, usually known as the nonce. Let’s keep this term in mind.

H is a one-way hash function and, in this case, we take advantage of the unpredictability of the result: it’s extremely difficult to correlate the input and the output of the function without applying H the input itself. In other words, without knowing the input, the output bits would appear as randomly picked making the sequence of EKs completely uncorrelated (and, in principle, killing any possibility of a statistical attack).

Another way to see this is that if we have input A and B and output C and D corresponding to A and B, we (actually nobody) would not be able to tell whether C = H(A) or C = H(B) without actually applying H.

It should also be noted that while H is unpredictable, it is also totally deterministic: applying H to the same input would
invariably yield the same output.

Racapping, the encryption scheme is the following:

The clearstream will be turned into the cipherstream via a XOR (⊕) operation with the so-called keystream, i.e. the sequence of the EKs.

We can also rewrite the previous scheme using some kind of formal notation:

It’s important to note that in such a scheme it’s of paramount importance to never repeat the same keystream for different sequence of packets. If that is the case, it would be possible to recover a XOR-combination of the clearstreams by leveraging the following properties of the XOR operation:

Bit 0 is the identity element, i.e. x ⊕ 0 = x.
Each bit is the inverse of itself, i.e. x ⊕ x = 0.
XOR is commutative, i.e. x ⊕ y = y ⊕ x, and distributive, i.e. (x ⊕ y) ⊕ z = x ⊕ (y ⊕ z) = x ⊕ y ⊕ z.

In practice, in any formula built out from solely XOR operations, it’s always possible to remove an even number of identical basic operands, whichever the position.

Hence, if two packets are encrypted using the same keystream, an attacker would be able to apply a XOR with the following result:

As already mentioned, the attacker is able to recover a XOR-combination of the two clearstreams which can be further (and more easily) analysed using statstical tools. It should be noted that this specific part of the KRACK attack is not innovative as it was long known.

With this pre-requisite in mind, understanding the inner working of the KRACK attack to WPA2 is relatively simple: in fact, it’s enough to force a WiFi device to re-use the same keystream, applying the trick should above in the final part.

How can this be done?

The KRACK attack shows that it’s possible to manipulate the flow of packets between two devices (namely the Access Point and the client) by mounting a man-in-the-middle attack — and in the article a particularly clever way to do so — to block the packet terminating the handshake so that it never reaches the Access Point.

At that point, the Access Point, according to the WPA2 specification, would resend the last-but-one packet of the handshake which, reaching the client, may force the reset of the nonce which, in turn, would trigger the re-use of the same keystream for the newly generated traffic. I want to underline the term “may” as the behaviour of the WPA2 client upon receiving again the last-but-one packet of the handshake protocol is not specified in the WPA2 itself, leaving this to interpretation. It turns out that most of the implementation of the WPA2 protocols actually resets the nonce.

Now for some considerations:

The vulnerability can easily be removed by forbidding the clients to reset the nonce — no need to revise the protocol.
In most of the cases, deciphering the traffic is not immediate as further statistical attacks (which may eventually be unsuccessful) are needed.
The communications with an HTTPS server (e.g. with your Bank) are protected by an additional layer, i.e. TLS, which is totally independent from WPA2.

What to do, then? Well, first of all, realising that explointing this vulnerability is not as easy as it seems from mainstream news and, under no circumstances, it leads to a compromise of the PSK. In addition, it cannot be mounted from a remote location (i.e. the attacker must be physically present at the location where the attack takes place).

In the second place, patch your devices regularly and you’re pretty most done. And never consider WPA2 a way to protect your traffic from eavesdropper, but only a way to restrict access to the communication channel of your WiFi network. Any sensitive connection should be furtherly protected using additional and much stronger protocols like TLS or SSH.